Fenômeno de Gibbs

Como disse na aula, o fenômeno de Gibbs é a curiosa discrepância que surge nas descontinuidades quando comparamos funções descontínuas e suas séries de Fourier. Aqui estão todos os cálculos que fizemos, com esmero, ao contrário da minha lousa. 😀

Relembrando, o ponto chave foi considerar a série de Fourier  da função degrau no intervalo [-\pi,\pi]

f(x) = \left\{\begin{array}{rr} 1, & \quad 0 < x < \pi \\ -1, & \quad -\pi < x <0 \end{array}\right. 

 

Como a função é impar, terá apenas série em senos \displaystyle f(x) = \sum_k b_k\sin kx, sendo

\displaystyle b_k  = \frac{2}{\pi} \int_0^{-\pi} \sin kx \, dx =\frac{2}{k\pi}(1-\cos k\pi)  = \left\{\begin{array}{cl} \frac{4}{k\pi}, & \quad k\ {\rm impar} \\ 0, & \quad k\ {\rm par} \end{array}\right.

 

Nossa função degrau, portanto, pode ser representada pela série de Fourier

\displaystyle    f(x) = \frac{4}{\pi}\sum_{n=0}^\infty \frac{\sin (2n+1)x}{2n+1}

 

Abaixo vai o gráfico correspondente aos 5 primeiros termos dessa série

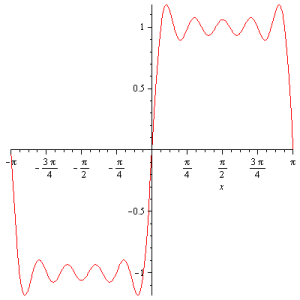
onde já podemos apreciar o fenômeno do “overshooting” na vizinhança da descontinuidade em   x=0. Consideremos agora as séries parciais correspondentes à série de Fourier

\displaystyle f_M(x) = \frac{4}{\pi}\sum_{n=0}^M \frac{\sin (2n+1)x}{2n+1}

 

A figura acima corresponde ao caso M=4. Vamos localizar os pontos críticos de f_M(x) no intervalo (0,\pi), que correspondem aos pontos tais que

  \displaystyle f'_M(x) = \frac{4}{\pi}\sum_{n=0}^M {\cos (2n+1)x} = 0 \quad\quad (1)

Notem que

\displaystyle \sum_{n=0}^M {\cos (2n+1)x} =\ {\rm Re}\left(\sum_{n=0}^M  e^{(2n+1)ix} \right) \quad\quad (2)

 

Desta forma, os zeros de (1) correspondem de fato aos zeros de (2). Ocorre que (2) pode ser facilmente somado, trata-se de uma PG complexa com razão e^{2ix}

\displaystyle \sum_{n=0}^M  e^{(2n+1)ix} = \frac{e^{ix}}{1-e^{2ix}}\left(1 - e^{2(M+1)ix} \right)

 

Porém, notem que

\displaystyle \frac{e^{ix}}{1-e^{2ix}} = \frac{1}{e^{-ix}-e^{ix}} = -\frac{1}{2i\sin x}

e

\displaystyle  1 - e^{2(M+1)ix} = e^{i(M+1)x}\left(e^{-i(M+1)x} -e^{i(M+1)x}\right)

 

\displaystyle = -2ie^{i(M+1)x} \sin(M+1)x

 

De onde temos finalmente que

\displaystyle  {\rm Re}\left(\sum_{n=0}^M  e^{(2n+1)ix} \right) = \frac{\sin(M+1)x}{\sin x} {\rm Re}\left(e^{i(M+1)x}\right) = \frac{\sin 2(M+1)x}{2\sin x}

implicando que os zeros de (2) no intervalo (0,1) , que serão os pontos críticos de (1) no mesmo intervalo, são os pontos x=\frac{k\pi}{2(M+1)} , com k=1,2,3,\dots . Do gráfico, vemos que o primeiro ponto crítico ( k=1 ) será um máximo localizado em x_* = \frac{\pi}{2(M+1)} .

Calculemos agora f_M(x_*)

\displaystyle f_M(x_*) = \frac{4}{\pi}\sum_{n=0}^M \frac{\sin (2n+1)x_*}{2n+1} =\frac{2}{\pi}\sum_{n=0}^M \frac{\pi}{M+1}\frac{\sin \alpha_n}{\alpha_n}

com \alpha_n = \frac{2n+1}{2M+2}\pi . Podemos calcular o limite M\to\infty desta soma se a aproximarmos por uma integral. Notem, primeiramente, que \alpha_0 = \frac{1}{2M+2}\pi , \alpha_M = \frac{2M+1}{2M+2}\pi e que   \alpha_{k+1} -\alpha_{k} = \frac{\pi}{M+1} . Em outras palavras, o intervalo (0,\pi) foi dividido em M+1 partes iguais (de fato, os extremos tem metade do tamanho), e estamos somando as áreas de retângulos de largura \frac{\pi}{M+1} e altura \frac{\sin\alpha_n}{\alpha_n} . A figura abaixo ilustra o caso para M=12 , sendo que a curva corresponde a função \frac{\sin x}{x}

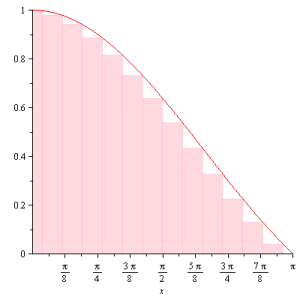
Teremos

\displaystyle \lim_{M\to\infty} f_M(x_*) = \frac{2}{\pi}\int_0^{\pi}\frac{\sin x}{x}\, dx \approx 1.179

 

que corresponde ao “overshoot”. Note que no limite M\to\infty, o ponto de máximo x_* está arbitrariamente próximo da descontinuidade x=0.  A figura abaixo ilustra o que ocorre para três valores de M: 4, 16 e 32. Ve-se claramente que o primeiro máximo varia pouco, mas sua localização se aproxima de x=0, de onde percebemos claramente o porquê da norma do L^2[-\pi,\pi] ser insensível a estas diferenças.

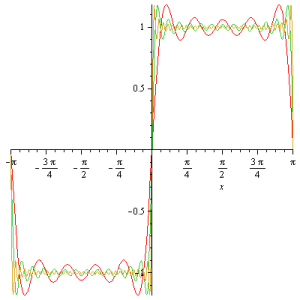
O fenômeno de Gibbs é caracterizado pelo valor relativo do “overshoot”, e não pelo absoluto como fizemos. No nosso caso, a descontinuidade é  f(0^+)-f(0^-)=2, então o “overshoot” relativo será

\frac{1.179 -1}{2}\approx 9\%

 

Que é o famoso resultado. A literatura a respeito é vastíssima. Sugiro este artigo, que é bem contextualizado historicamente e apresenta a derivação original, que não é a apresentada aqui. O resultado original foi deduzido não para a função degrau, mas para uma variação da “dente de serra“. O curioso, e interessantíssimo, é que o fenômeno (incluindo o 9%) é o mesmo para qualquer descontinuidade “razoável”. Isto quer dizer que, do ponto de vista das séries de Fourier, a descontinuidade estudada aqui é genérica. De fato, já discutimos que o ponto fundamental das descontinuidades é o decaimento dos coeficientes b_k. Aqui, como esperado, tratando-se de uma função descontínua, os coeficientes decaem como k^{-1}.

Como disse também, Michelson construiu um “computador analógico” para calcular séries de Fourier, e atribuiu erroneamente o fenômeno de Gibbs a um “defeito” mecânico de seu aparato. Mais informações sobre sua curiosa e engenhosa máquina aqui e aqui. Uma visão “mecânica” de como as componentes de Fourier interagem para gerar a função degrau é dada por esta (ótima!) animação, da wikipedia

 

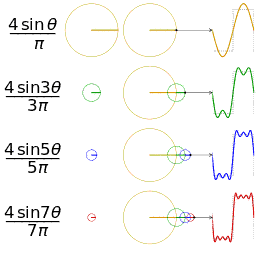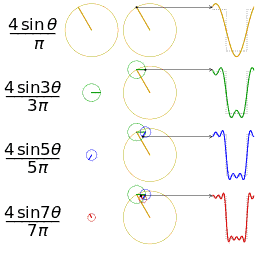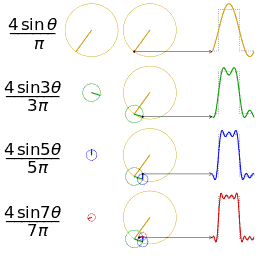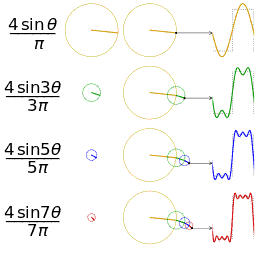
construida a partir do material apresentado aqui. Notem como os diversos modos de Fourier surgem ao combinarmos  epiciclos.  O video abaixo também é muito interessante.

Um último ponto para mostrar que a convergência pontual (quer dizer, com a norma do  L^\infty[-\pi,\pi]) é bastante complicada neste exemplo, surge ao considerarmos não o valor de f(x) no primeiro ponto fixo, mas em todos. Calculemos

\displaystyle f_M\left(x_*^{(k)} \right) =  \frac{2}{\pi}\sum_{n=0}^M \frac{k\pi}{M+1}\frac{\sin \alpha_n^k}{\alpha_n^k}

sendo    x_*^{(k)}=\frac{k\pi}{2M+2}  e   \alpha_n^{(k)} = \frac{2n+1}{2M+2}k\pi . Tomemos o limite M\to \infty , mantendo   k constante, de maneira análoga ao que fizemos para o caso k=1 acima

\displaystyle f\left(x_*^{(k)} \right) =  \frac{2}{\pi}\int_0^{k\pi} \frac{\sin x}{x}\, dx

Conhecemos esta integral. Seu limite para   k\to \infty (integral de Dirichlet) é exatamente \frac{\pi}{2}, de onde temos que, longe da singularidade ( k grandes), o valor de f\left(x_*^{(k)} \right) tende ao valor esperado f(x)=1. O gráfico abaixo mostra alguns valores de f\left(x_*^{(k)} \right) para k pequenos, de onde vemos que a convergência para o valor  f(x)=1 é o mesmo de uma série alternada.

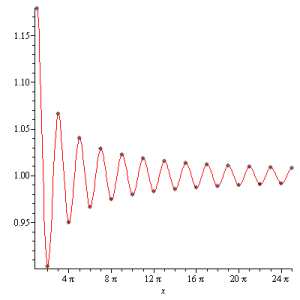
No limite M\to\infty pontos com k finito estão arbitrariamente próximos, sugerindo que a série de Fourier de f(x)é, de fato, complicadamente descontínua na região arbitrariamente próxima a x=0. Contudo, a norma do L^2[-\pi,\pi] é completamente insensível a este rico comportamento  próximo à descontinuidade x=0.