Month: August 2023

Como devemos interpretar  \displaystyle \delta'(x^2 -4) ? Aparentemente, há dúvidas sobre isso. Lembrando, as derivadas de delta são definidas como

\displaystyle \int \delta'(x) f(x) dx = -\int \delta(x) f'(x) dx

mas no nosso exemplo o argumento da delta é uma função. O que fazer? Bem, devemos fazer uma mudança de variáveis.  Vamos introduzir a variável \displaystyle y = x^2 -4 e lembrar que quando x percorre a reta real, y vai de \infty a -4 e depois de -4 a \infty . Teremos

\displaystyle \int_{-\infty}^\infty \delta'(x^2 - 4) f(x) dx = \int_{-4}^\infty \delta'(y) f(-\sqrt{y +4}) \frac{ dy}{2\sqrt{y +4}}+\int_{-4}^\infty \delta'(y) f(\sqrt{y +4}) \frac{ dy}{2\sqrt{y +4}}

Pela definição, teremos

\displaystyle  \int_{-4}^\infty \delta'(y) f(\sqrt{y  +4}) \frac{ dy}{2\sqrt{y +4}} = -\frac{1}{2} \int_{-4}^\infty \delta (y)\frac{d}{dy}\left(\frac{f(\sqrt{y +4})}{ \sqrt{ y+4}}\right)  dy  =  -\frac{1}{2} \int_{-4}^\infty \delta (y)   \left( \frac{f'(\sqrt{y +4})}{2(y+4)} -\frac{f(\sqrt{y +4})}{2\sqrt{y+4}^3}   \right) dy = -\frac{f'(2)}{16} + \frac{f(2)}{32}

de onde o resultado do Wolfram Alpha segue facilmente.

(Post de contribuição do Mr. M).

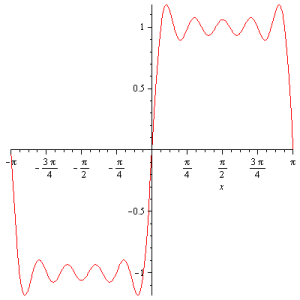
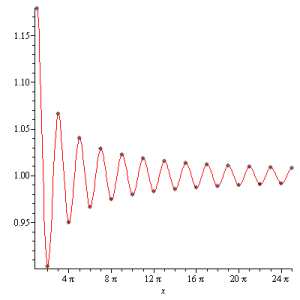
Vale a pena retornar ao problema da regra da cadeia com derivadas distribucionais. Vamos considerar o exemplo da função \displaystyle f(x) =\frac{\sin |x|}{x} comentada na aula passada.  O primeiro passo, sempre, para que não fique dúvidas, é inspecionar o gráfico da função, que vai abaixo. (Esse gráfico está no T2 de 2017.)

É evidente que há um salto na origem e, portanto, esperamos uma delta ai. Antes de passarmos ao cálculo da derivada distributiva, convém relembrarmos parte da discussão que foi motivada pela questão do Gustavo. Considerem a função

f(x) = \left\{ \begin{array}{rl}-\frac{\sin x}{x}, & x <0, \\a+\frac{\sin x}{x}, & x > 0.\end{array}\right.

 

A  derivada usual dessa função é

f'(x) = \left\{ \begin{array}{cl}-\left(\frac{\cos x}{x} - \frac{\sin x}{x^2} \right), & x <0, \\ \frac{\cos x}{x} - \frac{\sin x}{x^2} , & x > 0.\end{array}\right.

 

Como vocês vêm, a derivada não depende de a, ou, em palavras, a derivada usual não tem informação sobre a amplitude do salto.  A pergunta que colocamos em sala foi: dada essa derivada usual, podemos integrá-la e obter uma f(x) ? A resposta é, claramente, sim. Que função obteríamos? Bem, isso vai depender de algumas hipóteses extras. Primeiro, sabemos que essa pergunta sempre é respondida a menos de uma constante que deve ser obtida fixando-se f(x) para algum valor de x . As funções  f(x)   e  f(x) +c, com c constante, sempre têm a mesma derivada.   Sempre temos que fixar a constante de integração c com alguma informação sobre f(x). Essa é a única informação que precisamos fixar para obter f(x) a partir de f'(x) ? A resposta é não. Notem que todas as funções neste exemplo não estão definidas em x=0 . Portanto, há uma arbitrariedade aqui. Caso exijamos que f(x) seja contínua, que é uma hipótese extra ao problema, podemos sim obter de maneira única f(x)   a partir de f'(x) , a menos da dependência trivial na constante de integração c . Com a hipótese de continuidade em x=0 de f(x) , vamos obter a função que corresponde a a=-1 , convençam-se disso! Sem essa hipótese, não há como “emendar” a solução do lado esquerdo com a do lado direito, como fizemos em sala para um outro exemplo.  O que o caso a=-1 tem de especial? É o caso sem salto! Portanto, é o caso em que não perdemos nenhuma informação ao calcularmos a derivada, ao contrário de qualquer outro valor de a\ne -1 , quando vamos ter um salto que não ficará “registrado” na derivada. As derivadas distribucionais são as que “registram” as informações sobre as descontinuidades da função.

Vamos voltar ao problema inicial de determinar a derivada distribucional de \displaystyle f(x) =\frac{\sin |x|}{x} .  Há, no mínimo, 3 maneiras diferentes de se representar essa função:

\displaystyle f(x) =\frac{\sin |x|}{x} = \text{sign}\,x \frac{\sin x}{x} =  \frac{\sin x}{|x|} 

 

Obviamente, vamos obter a mesma derivada distribucional para as três expressões para f(x). Vamos começar pela que talvez seja a mais simples, a do gabarito do T2 de 2017.

\displaystyle \frac{d f(x)}{dx} = \frac{d }{dx} \left( \text{sign}\,x \frac{\sin x}{x}\right)   = 2 \delta(x) + \text{sign}\,x \left(\frac{\cos x}{x} - \frac{\sin x}{x^2} \right) \displaystyle= 2 \delta(x) + \frac{ |x|\cos x - \sin |x|}{x^2} 

 

sendo que usamos que \frac{d }{dx} \text{sign}\,x = 2\delta(x) e que \frac{\sin x}{x} , que formalmente não está definida na origem, tem uma extensão continua tal que seu valor é 1 na origem.

Porém, poderíamos ter escolhido outra expressão para a função, por exemplo

\displaystyle \frac{d f(x)}{dx} = \frac{d }{dx} \left(\frac{\sin |x|}{x}\right)   =  \frac{\cos |x|}{x} \frac{d|x| }{dx} - \frac{\sin |x|}{x^2}  \displaystyle =\frac{\cos |x|}{x}\left(  \text{sign}\,x + 2x\delta(x)\right)- \frac{\sin |x|}{x^2} = 2 \delta(x) + \text{sign}\,x \left(\frac{\cos x}{x} - \frac{\sin x}{x^2} \right)  

Aqui, usamos que \cos |x| = \cos x ,  |x| = x\text{sign}\, x  e que \frac{d|x|}{dx} = \text{sign}\,x + 2x\delta(x)  . Alguém por objetar aqui: mas não concluímos que x\delta(x) (a “distribuição M”)  era zero? Sim, mas aqui não temos essa distribuição, mas ela multiplicada por \frac{\cos x}{x}, vejam com cuidado e lembre-se sempre da construção dos aproximantes.

Temos o último caso

\displaystyle \frac{d f(x)}{dx} = \frac{d }{dx} \left(  \frac{\sin x}{|x|}\right)   = \frac{\cos x}{|x|} + \sin x  \frac{d}{dx}\left( \frac{1}{|x|}\right)

 

e agora teremos um problema com o último termo, que imagino ser a principal dúvida naquela questão do T2 de 2017.  Se admitirmos, o que é correto, que \displaystyle \frac{1}{|x|} = \frac{\text{sign\,}x}{x} , teremos

\displaystyle \frac{d}{dx}\left( \frac{1}{|x|}\right)= \frac{d}{dx}\left( \frac{\text{sign\,}x}{x} \right) = \frac{2\delta(x)}{x} - \frac{\text{sign\,}x}{x^2} .

 

que é o resultado anterior. Porém, poderíamos ter admitido, o que também é perfeitamente correto, que \displaystyle \frac{1}{|x|} = \frac{1}{x \text{sign\,}x}

e nesse caso teríamos

\displaystyle \frac{d}{dx}\left( \frac{1}{|x|}\right)= \frac{d}{dx}\left( \frac{1}{x\text{sign\,}x} \right) = -\frac{2\delta(x)}{x} - \frac{\text{sign\,}x}{x^2} . 😨

Obtemos o salto com o sinal errado!!!! 😨 Como sabemos que o salto está com o sinal errado? Pois nós sabemos do gráfico da função que o salto é de -1 a 1, confiram!

O que está errado?!?! Bem, o erro está neste passo que foi implicitamente usado:

\displaystyle \frac{d}{dx}\left( \frac{1}{\text{sign\,}x}\right)= -\frac{1}{(\text{sign\,}x)^2} \frac{d}{dx} \text{sign\,}x = - 2\delta(x)

 

Como eu sei que esse passo está errado? Como sempre, vamos ver nossos aproximantes. O melhor aproximante pra função sinal (ou pra a de Heaviside) é a tangente hiperbólica

\displaystyle  \text{sign\,}x = \lim_{n\to\infty}\tanh nx

 

Convençam-se que esses aproximantes não suportam a conclusão acima, pois \displaystyle \frac{1}{(\text{sign\,}x)^2} \frac{d}{dx} \text{sign\,}x não está definido na origem.  A função sinal, para efeitos distribucionais é definida como \displaystyle  \text{sign\,}x = \frac{1}{\text{sign\,}x} e, portanto,

\displaystyle \frac{d}{dx}\left( \frac{1}{\text{sign\,}x}\right)=  \frac{d}{dx} \text{sign\,}x =  2\delta(x) 😀

Que isso sirva de alerta: as propriedades das derivadas distribucionais podem ser bastante traiçoeiras. Na dúvida, sempre apelem aos aproximantes.

Como disse na aula, o fenômeno de Gibbs é a curiosa discrepância que surge nas descontinuidades quando comparamos funções descontínuas e suas séries de Fourier. Aqui estão todos os cálculos que fizemos, com esmero, ao contrário da minha lousa. 😀

Relembrando, o ponto chave foi considerar a série de Fourier  da função degrau no intervalo [-\pi,\pi]

f(x) = \left\{\begin{array}{rr} 1, & \quad 0 < x < \pi \\ -1, & \quad -\pi < x <0 \end{array}\right. 

 

Como a função é impar, terá apenas série em senos \displaystyle f(x) = \sum_k b_k\sin kx, sendo

\displaystyle b_k  = \frac{2}{\pi} \int_0^{-\pi} \sin kx \, dx =\frac{2}{k\pi}(1-\cos k\pi)  = \left\{\begin{array}{cl} \frac{4}{k\pi}, & \quad k\ {\rm impar} \\ 0, & \quad k\ {\rm par} \end{array}\right.

 

Nossa função degrau, portanto, pode ser representada pela série de Fourier

\displaystyle    f(x) = \frac{4}{\pi}\sum_{n=0}^\infty \frac{\sin (2n+1)x}{2n+1}

 

Abaixo vai o gráfico correspondente aos 5 primeiros termos dessa série

onde já podemos apreciar o fenômeno do “overshooting” na vizinhança da descontinuidade em   x=0. Consideremos agora as séries parciais correspondentes à série de Fourier

\displaystyle f_M(x) = \frac{4}{\pi}\sum_{n=0}^M \frac{\sin (2n+1)x}{2n+1}

 

A figura acima corresponde ao caso M=4. Vamos localizar os pontos críticos de f_M(x) no intervalo (0,\pi), que correspondem aos pontos tais que

  \displaystyle f'_M(x) = \frac{4}{\pi}\sum_{n=0}^M {\cos (2n+1)x} = 0 \quad\quad (1)

Notem que

\displaystyle \sum_{n=0}^M {\cos (2n+1)x} =\ {\rm Re}\left(\sum_{n=0}^M  e^{(2n+1)ix} \right) \quad\quad (2)

 

Desta forma, os zeros de (1) correspondem de fato aos zeros de (2). Ocorre que (2) pode ser facilmente somado, trata-se de uma PG complexa com razão e^{2ix}

\displaystyle \sum_{n=0}^M  e^{(2n+1)ix} = \frac{e^{ix}}{1-e^{2ix}}\left(1 - e^{2(M+1)ix} \right)

 

Porém, notem que

\displaystyle \frac{e^{ix}}{1-e^{2ix}} = \frac{1}{e^{-ix}-e^{ix}} = -\frac{1}{2i\sin x}

e

\displaystyle  1 - e^{2(M+1)ix} = e^{i(M+1)x}\left(e^{-i(M+1)x} -e^{i(M+1)x}\right)

 

\displaystyle = -2ie^{i(M+1)x} \sin(M+1)x

 

De onde temos finalmente que

\displaystyle  {\rm Re}\left(\sum_{n=0}^M  e^{(2n+1)ix} \right) = \frac{\sin(M+1)x}{\sin x} {\rm Re}\left(e^{i(M+1)x}\right) = \frac{\sin 2(M+1)x}{2\sin x}

implicando que os zeros de (2) no intervalo (0,1) , que serão os pontos críticos de (1) no mesmo intervalo, são os pontos x=\frac{k\pi}{2(M+1)} , com k=1,2,3,\dots . Do gráfico, vemos que o primeiro ponto crítico ( k=1 ) será um máximo localizado em x_* = \frac{\pi}{2(M+1)} .

Calculemos agora f_M(x_*)

\displaystyle f_M(x_*) = \frac{4}{\pi}\sum_{n=0}^M \frac{\sin (2n+1)x_*}{2n+1} =\frac{2}{\pi}\sum_{n=0}^M \frac{\pi}{M+1}\frac{\sin \alpha_n}{\alpha_n}

com \alpha_n = \frac{2n+1}{2M+2}\pi . Podemos calcular o limite M\to\infty desta soma se a aproximarmos por uma integral. Notem, primeiramente, que \alpha_0 = \frac{1}{2M+2}\pi , \alpha_M = \frac{2M+1}{2M+2}\pi e que   \alpha_{k+1} -\alpha_{k} = \frac{\pi}{M+1} . Em outras palavras, o intervalo (0,\pi) foi dividido em M+1 partes iguais (de fato, os extremos tem metade do tamanho), e estamos somando as áreas de retângulos de largura \frac{\pi}{M+1} e altura \frac{\sin\alpha_n}{\alpha_n} . A figura abaixo ilustra o caso para M=12 , sendo que a curva corresponde a função \frac{\sin x}{x}

Teremos

\displaystyle \lim_{M\to\infty} f_M(x_*) = \frac{2}{\pi}\int_0^{\pi}\frac{\sin x}{x}\, dx \approx 1.179

 

que corresponde ao “overshoot”. Note que no limite M\to\infty, o ponto de máximo x_* está arbitrariamente próximo da descontinuidade x=0.  A figura abaixo ilustra o que ocorre para três valores de M: 4, 16 e 32. Ve-se claramente que o primeiro máximo varia pouco, mas sua localização se aproxima de x=0, de onde percebemos claramente o porquê da norma do L^2[-\pi,\pi] ser insensível a estas diferenças.

O fenômeno de Gibbs é caracterizado pelo valor relativo do “overshoot”, e não pelo absoluto como fizemos. No nosso caso, a descontinuidade é  f(0^+)-f(0^-)=2, então o “overshoot” relativo será

\frac{1.179 -1}{2}\approx 9\%

 

Que é o famoso resultado. A literatura a respeito é vastíssima. Sugiro este artigo, que é bem contextualizado historicamente e apresenta a derivação original, que não é a apresentada aqui. O resultado original foi deduzido não para a função degrau, mas para uma variação da “dente de serra“. O curioso, e interessantíssimo, é que o fenômeno (incluindo o 9%) é o mesmo para qualquer descontinuidade “razoável”. Isto quer dizer que, do ponto de vista das séries de Fourier, a descontinuidade estudada aqui é genérica. De fato, já discutimos que o ponto fundamental das descontinuidades é o decaimento dos coeficientes b_k. Aqui, como esperado, tratando-se de uma função descontínua, os coeficientes decaem como k^{-1}.

Como disse também, Michelson construiu um “computador analógico” para calcular séries de Fourier, e atribuiu erroneamente o fenômeno de Gibbs a um “defeito” mecânico de seu aparato. Mais informações sobre sua curiosa e engenhosa máquina aqui e aqui. Uma visão “mecânica” de como as componentes de Fourier interagem para gerar a função degrau é dada por esta (ótima!) animação, da wikipedia

 

construida a partir do material apresentado aqui. Notem como os diversos modos de Fourier surgem ao combinarmos  epiciclos.  O video abaixo também é muito interessante.

Um último ponto para mostrar que a convergência pontual (quer dizer, com a norma do  L^\infty[-\pi,\pi]) é bastante complicada neste exemplo, surge ao considerarmos não o valor de f(x) no primeiro ponto fixo, mas em todos. Calculemos

\displaystyle f_M\left(x_*^{(k)} \right) =  \frac{2}{\pi}\sum_{n=0}^M \frac{k\pi}{M+1}\frac{\sin \alpha_n^k}{\alpha_n^k}

sendo    x_*^{(k)}=\frac{k\pi}{2M+2}  e   \alpha_n^{(k)} = \frac{2n+1}{2M+2}k\pi . Tomemos o limite M\to \infty , mantendo   k constante, de maneira análoga ao que fizemos para o caso k=1 acima

\displaystyle f\left(x_*^{(k)} \right) =  \frac{2}{\pi}\int_0^{k\pi} \frac{\sin x}{x}\, dx

Conhecemos esta integral. Seu limite para   k\to \infty (integral de Dirichlet) é exatamente \frac{\pi}{2}, de onde temos que, longe da singularidade ( k grandes), o valor de f\left(x_*^{(k)} \right) tende ao valor esperado f(x)=1. O gráfico abaixo mostra alguns valores de f\left(x_*^{(k)} \right) para k pequenos, de onde vemos que a convergência para o valor  f(x)=1 é o mesmo de uma série alternada.

No limite M\to\infty pontos com k finito estão arbitrariamente próximos, sugerindo que a série de Fourier de f(x)é, de fato, complicadamente descontínua na região arbitrariamente próxima a x=0. Contudo, a norma do L^2[-\pi,\pi] é completamente insensível a este rico comportamento  próximo à descontinuidade x=0.